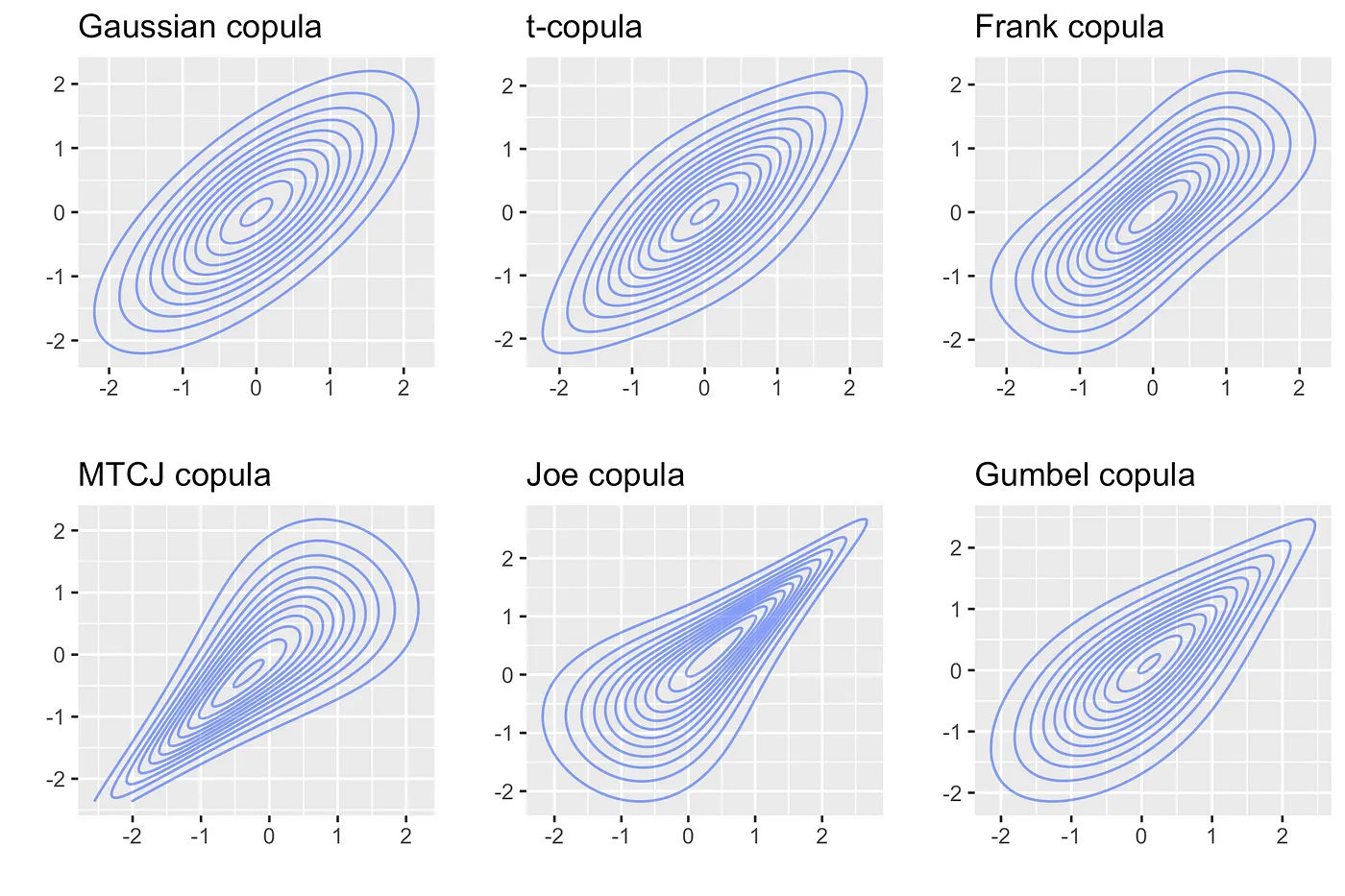
Introduction to Copulas
This article is a high level overview of some of the concepts mentioned on this Wiki Page on probability theory.
Copulas are important functions that explain the dependence between 2 or more random variables.
Common uses can be found within risk management, portfolio optimization problems, derivatives pricing, climate/weather predictions and signal processing.
More recently copulas are being used within machine learning to help generate synthetic tabular data. Using a copula you can train a model to recognize the statistical properties of a dataset and then sample from the trained model to produce “synthetic” data which in theory, maintains the same statistical properties as the original dataset.
In this article I will review the basic concept of copulas.
What is a copula?
The word copula means to “link/combine things together”. In probability theory, copulas are important functions that explain the dependance between 2 or more random variables. Specifically, they are used to combine individual “marginal” distributions of single random variables to arrive at the joint distribution of these variables.
Example Consider 2 random variables: X₁ and X₂
Case 1: X₁ and X₂ are independent.
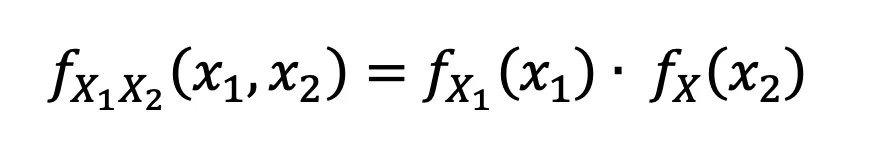 where f is the probability density function. So for the case that we have 2 independent variables, the joint distribution of these variables is simply the marginal density functions multiplied together.
where f is the probability density function. So for the case that we have 2 independent variables, the joint distribution of these variables is simply the marginal density functions multiplied together.
Case 2: X₁ and X₂ are dependent + we know the distributions of X₁ and X₂ (e.g gaussian).
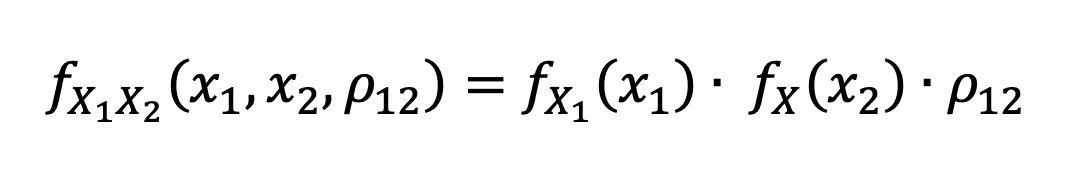 . In the case that we know the distributions of x1 and x2, then we can simply look up from literature the correlation function ρ12 that explains the dependence that x1 and x2 have.
. In the case that we know the distributions of x1 and x2, then we can simply look up from literature the correlation function ρ12 that explains the dependence that x1 and x2 have.
Case 3: X₁ and X₂ are Dependent + ?? no information about their distributions.
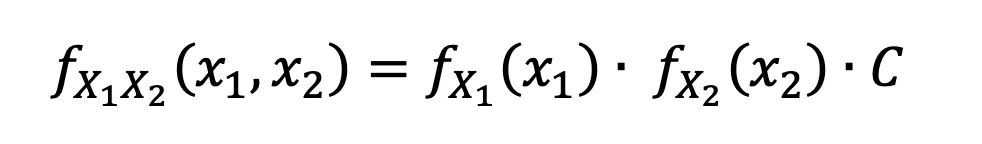 . In the case that we don’t know the distributions of our random variables x1 and x2, then all we can say is that there must be some copula function C that explains their dependence even if we don’t know it yet.
. In the case that we don’t know the distributions of our random variables x1 and x2, then all we can say is that there must be some copula function C that explains their dependence even if we don’t know it yet.
The equation in case 3 is known as Sklar’s Theorem, which simply states that the joint distribution of 2 random variables is simply the product of their marginals x copula.
In summary so far:
A copula is a function that contains the dependence information between 2 or more random variables and tells you how they are correlated.
Marginal distributions x copula = Joint Distribution
Probability Density Function
Even though I’ve only mentioned the probability density function (PDF) when talking about joint and marginal distributions, if someone asks for the joint distribution between 2 variables you could also answer using the correlated density function (CDF). For simplicity we’ll denote the difference using f or F respectively:
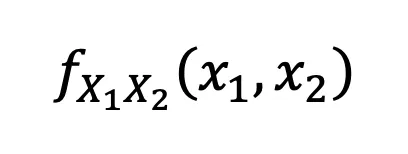
Correlated Density Function
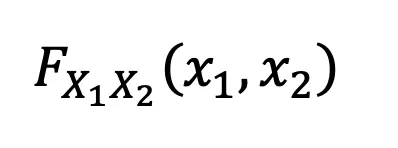 where PDF is the derivative of the CDF.
where PDF is the derivative of the CDF.
Cross Applying Copulas and Mapping
Because copulas only contain the dependence information, they are not specific to any particular random variables. Therefore you can apply copulas to other families “domains”. This is an important property since it allows you to apply the same copula to other data you suspect might have similar dependence properties as another dataset.
In the case that we want to use variables of some domain (X₁ and X₂) and apply a copula to them from another domain then we must first map the variables to the new domain. X₁ → Y₁ & X₂ → Y₂.
Example
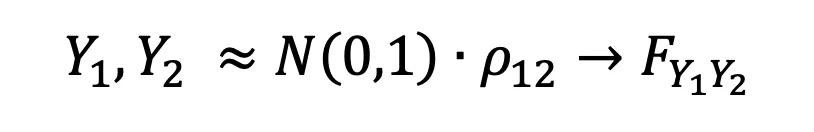 where Y1 and Y2 are normally distributed and linked by some correlation function ρ12.
where Y1 and Y2 are normally distributed and linked by some correlation function ρ12.
How we Map (Mapping X₁ → Y₁) —>
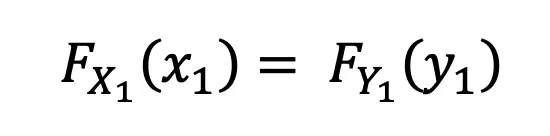
We set both CDFs equal to each other. Since we already know the CDF of the original domain and we know the CDF of the new domain but not the value y₁, the problem simply boils down to “for what value y1 do we need to get the same CDF as the left”.
Therefore y₁ is simply the inverse of the normal function:
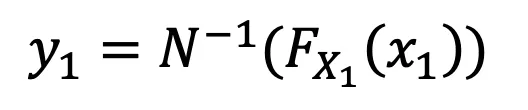 The same can be done for X₂ → Y₂ and the final mapping becomes:
The same can be done for X₂ → Y₂ and the final mapping becomes:
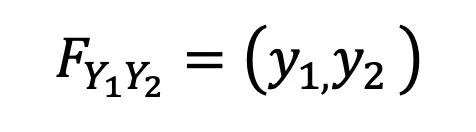 which is now a known function and called the “Gaussian copula”.
which is now a known function and called the “Gaussian copula”.